Description du module d'optimisation
Le module d'optimisation de MSE permet de minimiser une fonction paramétrée nommée 
:
Dans MSE, l'évaluation de est le résultat de l'appel au simulateur et de la fonction de contraste.
Algorithme de Quasi-Newton contraint
Description
Les algorithmes de Quasi-Newton construisent une suite 
qui convergent vers un extremum local de . Pour le calcul de 
, l'algorithme a besoin des valeurs de la fonction et de ses gradients. Le calcul des variations de peuvent être calculés par différences finies ; cette approche conduit à un grand nombre d'appels au simulateur, rendant l'algorithme lent et imprécis. Une autre approche, implémentée dans MSE, met en oeuvre un algorithme inspiré de la Différentiation Algorithmique, qui calcule les variations de pour un coût calculatoire marginal. Cette implémentation est détaillée dans le document 'aspect numérique'.
MSE utilise N2QN1.
Mise en oeuvre dans MSE
L'élément d'interface ci-dessous permet de modifier les paramètres de l'optimisation.
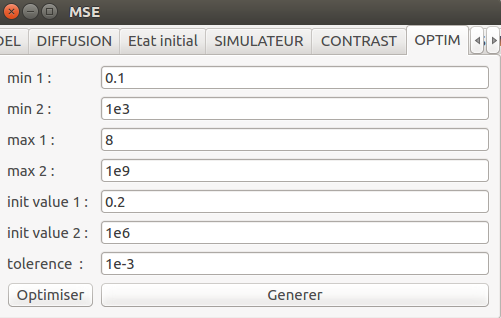
En python, le paramétrage se fait de la façon suivante:
mse.setBfgsLowerBound(0,0.1)
#borne inf du second paramétre
mse.setBfgsLowerBound(1,1e3)
#borne sup du premier paramétre
mse.setBfgsUpperBound(0,8)
#borne sup du second paramétre
mse.setBfgsUpperBound(1,1e10)
#Point de départ de l'algorithme
mse.setBfgsInitialState(0,0.2)
mse.setBfgsInitialState(1,1e6)
#Tolérence de convergence
mse.setBfgsTol(1e-3)
#génération des éléments nécessaires à l'optimisation
mse.buildBfgs()
L'optimisation se lance dans le répertoire de travail par la commande optim. Le tutoriel 'Estimation des paramètres de diffusion et de réaction sur les données de la grippe' illustre la mise en oeuvre de l'optimisation dans MSE.
Couplage à Matlab
Il est possible de coupler le simulateur à l'optimiseur Matlab de la façon suivante:
Créer une fonction appelant le simulateur, fichier callF.m:
function LikeLihood=callFF(P)% call Freefem
fileID = fopen('modelParams.edp','w');
fprintf(fileID,'POptim(0)=%.15f;\n',P(1)); fprintf(fileID,'p1=%.15f;\n',P(1));
fprintf(fileID,'POptim(1)=%.15f;\n',P(2));fprintf(fileID,'p2;=%.15f;\n',P(1));
fclose(fileID);
MatlabPath = getenv('LD_LIBRARY_PATH');
setenv('LD_LIBRARY_PATH','/usr/local/lib:/usr/lib:');
system('FreeFem++-nw main.edp ');
setenv('LD_LIBRARY_PATH',MatlabPath);
fileRES = fopen('mesure.txt','r');
LikeLihood = fscanf(fileRES,'%f');
fclose(fileRES);
Appeler l'algorithme d'optimisation optim.m:
x0=[-5 1 ];
bl=[-7 -1 ]; % lower bound
bm=[-4 4]; % upper bound
for i=1:1
options = optimset('Display','iter');
%minimisation sous contrainte
[xopt , fopt , exitflag] = fmincon('callFF',x0,[],[],[],[],bl,bm,[],options);
namesave=['result_' num2str(i)];
save(namesave,'x0','xopt','fopt')
x0=bl+rand(1,6).*(bm-bl);
end