Description du module d'inférence bayésienne
Les données (bruitées, dégradées, agrégées, non exhaustives, censurées etc.) sont des fonctions aléatoires de l'évolution spatio-temporelle de la densité réelle de la population.
Dans ce contexte, nous proposons de construire un modèle du processus d'observation qui soit conditionnel au modèle mécaniste et qui décrit le lien stochastique entre la densité de population et les données.
L'estimation des paramètres est réalisée à l'aide d'une méthode statistique. Dans le cas présent, il s'agit d'inférence bayésienne (plus d'informations sur le site web Biobayes).
Nous construisons ainsi un modèle hiérarchique composé :
(1) d'un modèle a priori pour les paramètres (lois définissant les paramètres theta),
(2) d'un modèle mécaniste de la dynamique (processus latent Z conditionné par les paramètres) et
(3) d'un modèle du processus d'observation (loi décrivant les données sachant le processus latent et les paramètres).
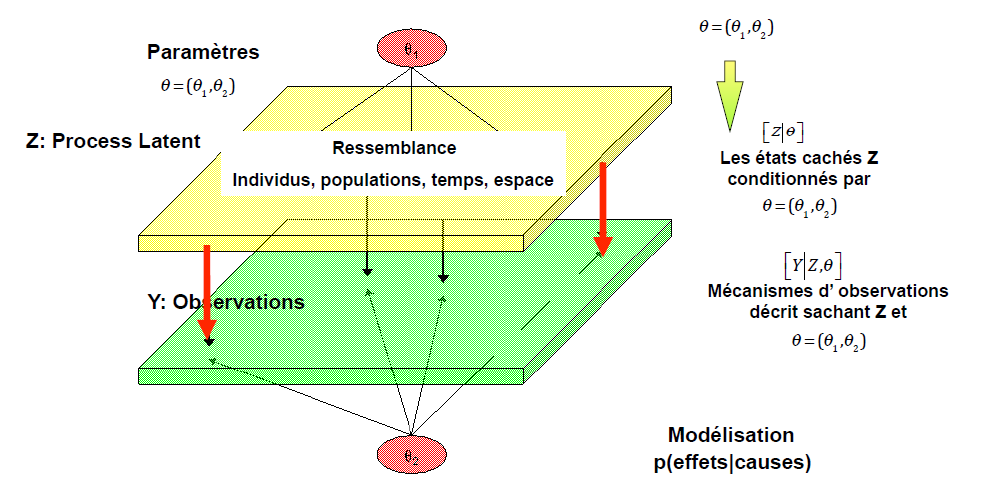
Figure : schéma de modélisation hiérarchique (source : Eric Parent)
Ce modèle hiérarchique peut aussi être représenté sous la forme d'un graphe acyclique orienté (ci dessous).
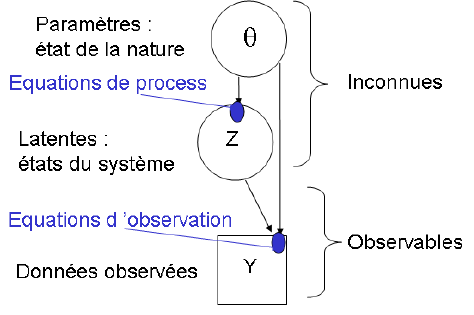
Figure : Graphe acyclique orienté (DAG) (source : Eric Parent)
Mise en oeuvre dans MSE
interface homme-machine
Le modèle (script JAGS) sera composé de 3 parties :
- la définition de lois a priori pour les paramètres
- une fonction d'appel au simulateur (modèle dynamique résolu ici par FreeFem++) permettant la récupération des sorties (valeurs de densité)
- le calcul de la vraisemblance des paramètres du modèle par rapport aux données.
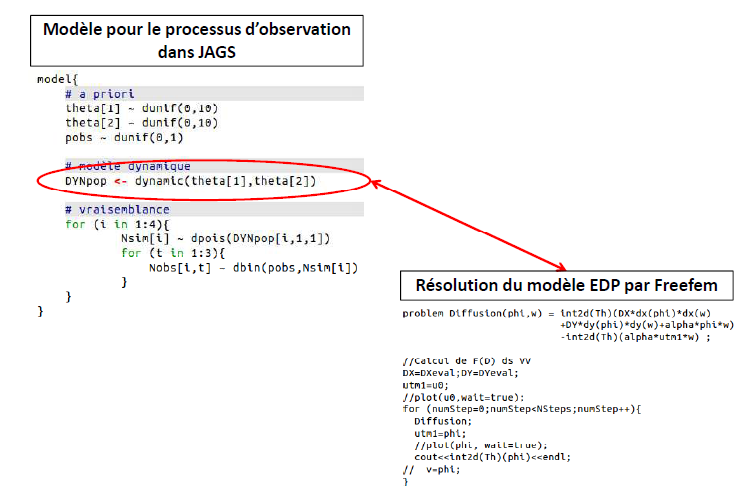
Figure : Exemple de script de modèle JAGS avec appel au simulateur (Freefem++ dans ce cas)
paramètres tuning (niter..)
Résultats
L'algorithme développé dans JAGS (échantillonneur de Gibbs) permet de calculer les densités a posteriori des paramètres du modèle.
