Introduction
Ce tutoriel montre comment estimer de coefficients de diffusion anisotrope. Les deux paramètres (p1,p2) représentent les coefficients de diffusion selon les directions des abscisses et des ordonnées. Les valeurs de ces paramètres sont déterminées en minimisant l'intégrale de l'erreur quadratique entre la simulation et les données.
La suite de cette page décrit comment mener cette étude dans MSE, d'une part via l'interface, d'autre part via un script python.
Description de l'étude
Il s'agit donc d'une étude portant sur 1 espèce et 2 paramètres :
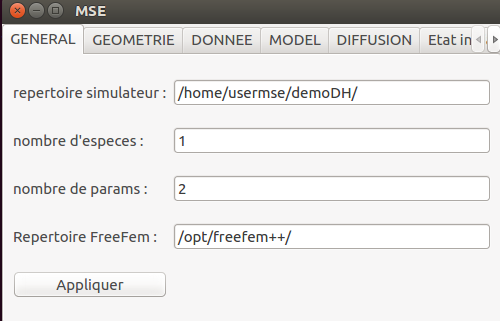
import mse
MY_OUTPUT_DIR=os.getenv("MSE_OUTPUT_DIR", "/home/usermse/demoDH/")
mse.setStringParam(mse.MSE_KEY_OUTPUT_DIR,MY_OUTPUT_DIR)
mse.setIntParam(mse.MSE_KEY_MODEL_NBSPECIES,1)
mse.setIntParam(mse.MSE_KEY_MODEL_NBPARAMS,2)
mse.initGradEdp()
mse.initModel()
Description de la zone d'étude
La zone d'étude est le carré [-1,1]2. La triangulation sera créer à partir de 30 points par unité de longueur des arêtes :
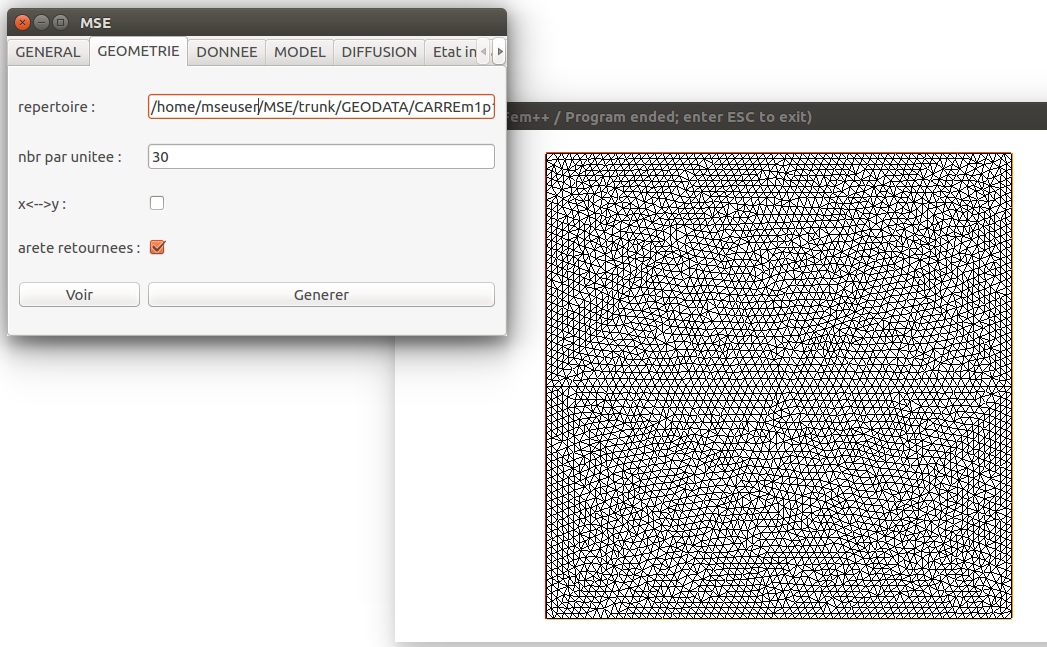
mse.setStringParam(mse.MSE_KEY_GEOM_DIR,MY_GEOM_DIR)
mse.setRealParam(mse.MSE_KEY_GEOM_NPERLENGTH,30.0)
mse.setIntParam(mse.MSE_KEY_GEOM_SYM,0)
mse.setIntParam(mse.MSE_KEY_GEOM_REVEDGE,1)
mse.buildGeom()
mse.buildDirectories()
os.system("cd "+MY_OUTPUT_DIR+";/opt/freefem++/src/nw/FreeFem++-nw "+MY_OUTPUT_DIR+"/buildXY.edp")
Description du modèle de diffusion
Le modèle étudié ici est de la forme :
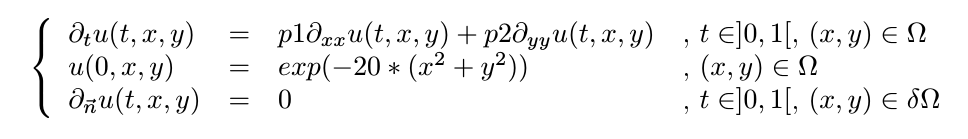
Définition de la diffusion hétérogène :
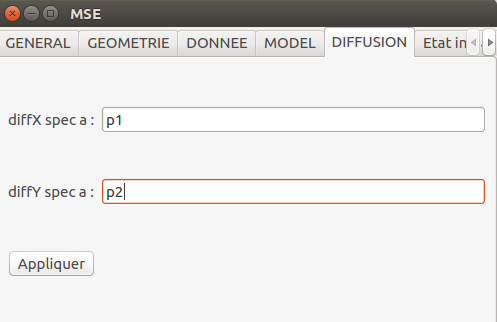
mse.setdpiDiffusionxExp(0,0,0,"1")
mse.setdpiDiffusionxExp(1,0,0,"0")
mse.setDiffusionyExp(0,0,"p2")
mse.setdpiDiffusionyExp(0,0,0,"0")
mse.setdpiDiffusionyExp(1,0,0,"1")
mse.buildDiffusion()
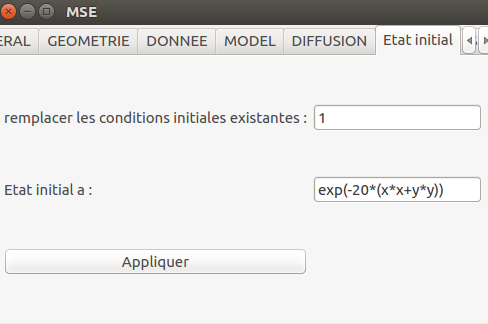
L'état initial est définie de la façon suivante :
mse.initInitialState()
mse.setIntParam(mse.MSE_KEY_FORCE_INITIAL_STATE,1)
mse.setInitialState(0,0,"exp(-20*(x*x+y*y))")
mse.setdPICiFj(0,0,"0")
mse.setdPICiFj(1,0,"0")
mse.printInitialState()
Définition des paramètres du simulateur
On choisit de simuler sur la période de temps [0,1], avec un pas de temps fixe égale à 0.05. La non-linéarité sera gérée par un algorithme de Newton-Raphson et une tolérance absolue de 0.02.
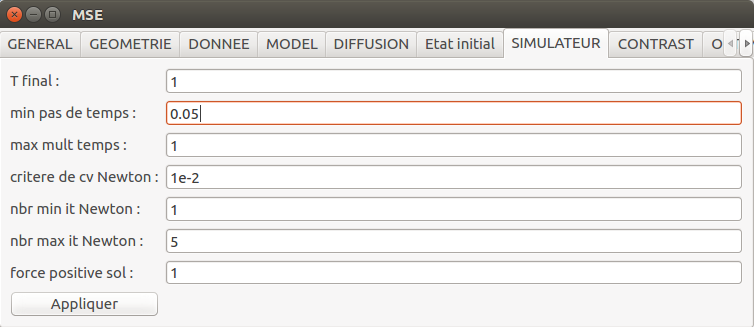
mse.setRealParam(mse.MSE_KEY_SIM_MINSTEP,0.05)
mse.setIntParam(mse.MSE_KEY_SIM_MAXMULTSTEP,1)
mse.setRealParam(mse.MSE_KEY_SIM_NEWTON_CRIT,0.01)
mse.setIntParam(mse.MSE_KEY_SIM_NEWTON_MIN_IT,1)
mse.setIntParam(mse.MSE_KEY_SIM_NEWTON_MAX_IT,5)
mse.setIntParam(mse.MSE_KEY_SIM_FORCE_POSITIV,1)
mse.buildTS()
Définition de la fonction objectif à minimiser
Il s'agit ici de minimiser l'intégrale de la différence quadratique entre la simulation et les données pour les pas de temps spécifiés.
La fonction de coût associée au paramètre (p1,p2) est:
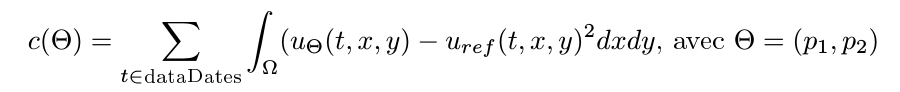
Avec uref la simulation servant de référence.
Cela se spécifie de la façon suivante dans l'interface :
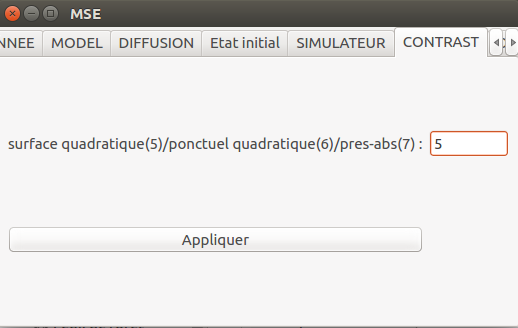
mse.buildContrast()
Description des données
Les dates d'observations sont précisées dans un fichier dataDates.txt qu'il faudra créer dans le répertoire de l'étude initialement spécifié "/home/mseuser/demoDH/PROCESSUS/DATA". Pour chaque date d'observation l'état du système doit être défini dans un fichier 0s02D0Ref.
Pour cet exemple, les données ont étés calculées à partir d'une simulation avec les paramètres (p1=0.2, p2=0.1).
Description du problème d'optimisation
Il s'agit d'un problème d'optimisation sous contraintes. Pour le résoudre, un algorithme de Quasi-Newton BFGS est couplé au simulateur. Il s'agit d'un algorithme itératif pour lequel le point de départ est précisé ainsi que les conditions de convergence :
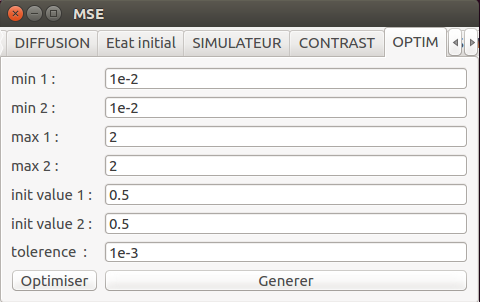
mse.setBfgsLowerBound(0,1e-2)
mse.setBfgsLowerBound(1,1e-2)
mse.setBfgsUpperBound(0,2.0)
mse.setBfgsUpperBound(1,2.0)
mse.setBfgsInitialState(0,0.5)
mse.setBfgsInitialState(1,0.5)
mse.setBfgsTol(1e-3)
mse.buildBfgs()
Résultat de l'optimisation
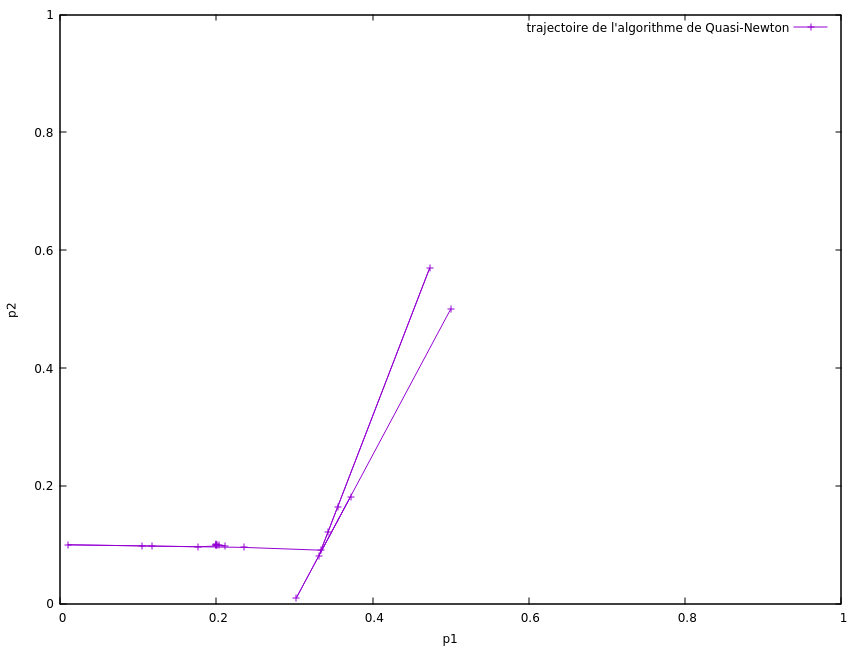
Il faut 20 appels au simulateur pour converger vers la valeur (p1=0.2, p2=0.1) à 10-6 près. Le graphique suivant représente la trajectoire des itérations de l'algorithme d'optimisation.
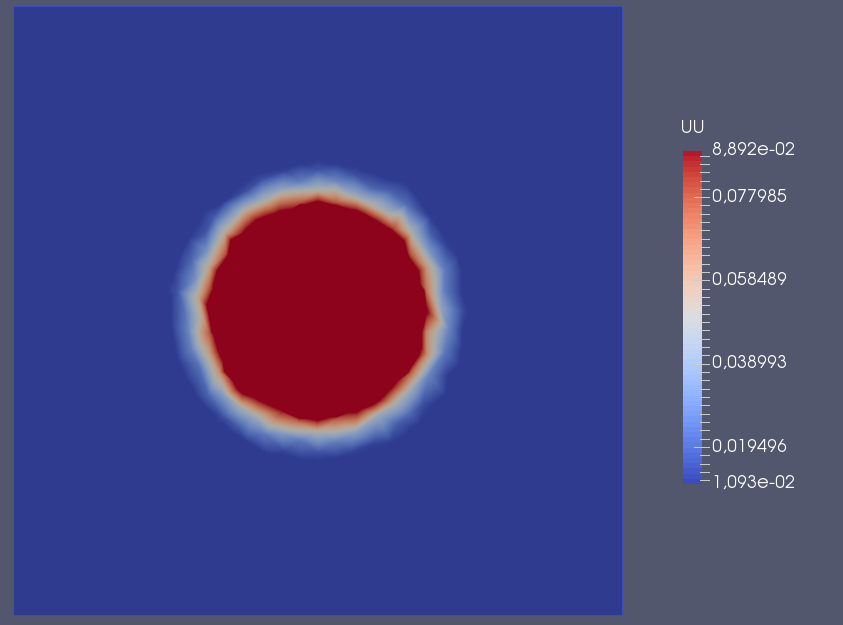
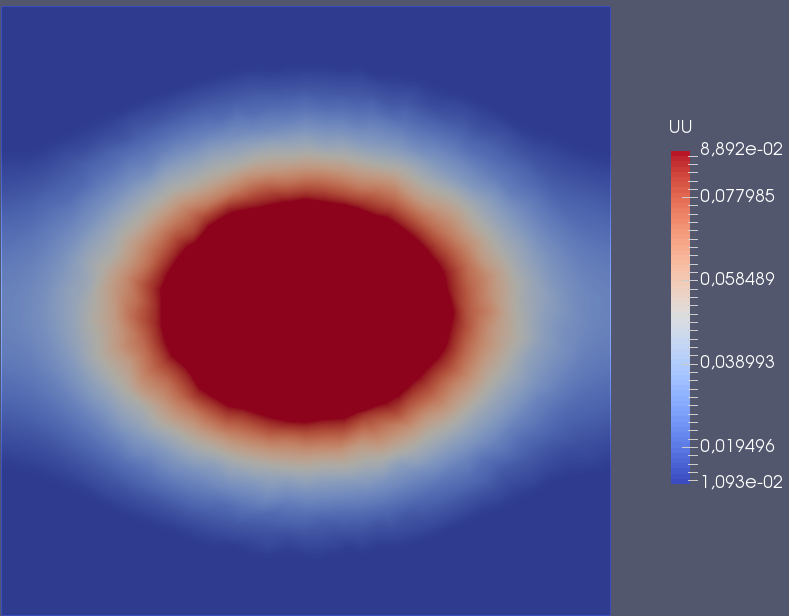
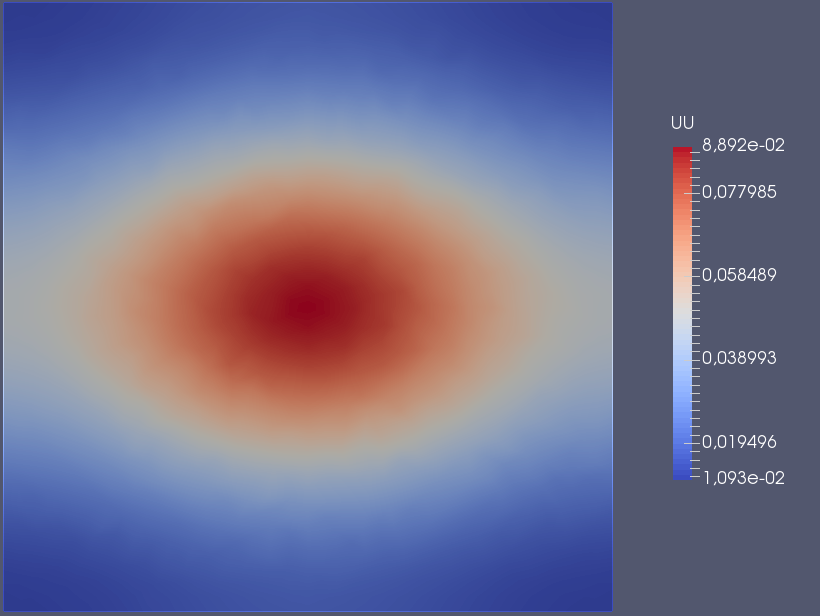
Images représentant l'état pour t=0, t=0.5 et t=1: