Introduction
Il s'agit de déterminer les caractéristiques du déplacement d'une population et le taux de détection du processus d'observation. Les 3 paramètres à estimer représentent les coefficients de diffusion selon les directions des abscisses et des ordonnées (p1,p2) et le taux de détection (p3). Le processus d'observation utilisé est un processus de détectabilité.
Cette page montre comment réaliser cette étude avec MSE, d'une part en utilisant l'interface et d'autre part en python.
Description de l'étude
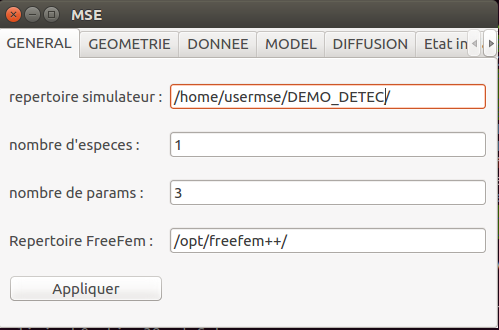
Il s'agit d'une étude portant sur 1 espèce et 3 paramètres :
import mse
MY_OUTPUT_DIR=os.getenv("MSE_OUTPUT_DIR", "/home/usermse/DEMO_DETEC/")
mse.setStringParam(mse.MSE_KEY_OUTPUT_DIR,MY_OUTPUT_DIR)
mse.setIntParam(mse.MSE_KEY_MODEL_NBSPECIES,1)
mse.setIntParam(mse.MSE_KEY_MODEL_NBPARAMS,3)
mse.initGradEdp()
mse.initModel()
Description de la zone d'étude
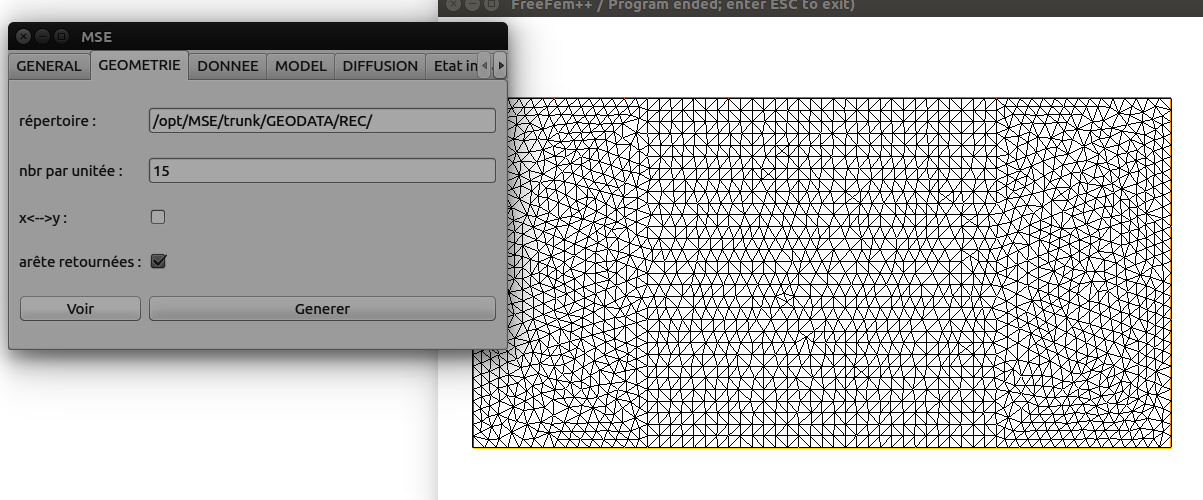
La zone d'étude est le rectangle [-2,2]x[-1,1]. La triangulation sera créée à partir de 15 points par unité de longueur des arêtes :
mse.setStringParam(mse.MSE_KEY_GEOM_DIR,MY_GEOM_DIR)
mse.setRealParam(mse.MSE_KEY_GEOM_NPERLENGTH,15.0)
mse.setIntParam(mse.MSE_KEY_GEOM_SYM,0)
mse.setIntParam(mse.MSE_KEY_GEOM_REVEDGE,1)
mse.buildGeom()
mse.buildDirectories()
os.system("cd "+MY_OUTPUT_DIR+";/opt/freefem++/src/nw/FreeFem++-nw "+MY_OUTPUT_DIR+"/buildXY.edp")
Description du modèle de diffusion
Dans le cas de captures à des moments précis, le modèle représente l'évolution de la densité de population au court du temps:
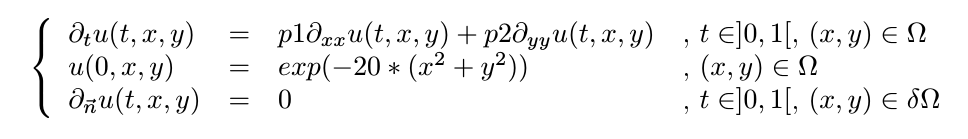
S'il s'agit de pièges posés à l'instant initial et opérant durant toute la période de l'étude, alors il convient de modéliser la densité cumulée dans le temps ![]() . Cela conduit au modèle suivant:
. Cela conduit au modèle suivant:
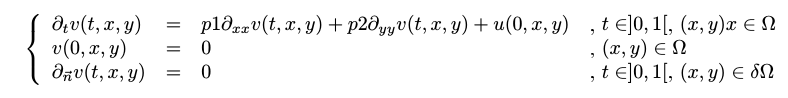
Il n'y a pas de terme source:
mse.setfxExp(0,"0")
mse.setdyfxExp(0,0,"0")
mse.setdPiFj(0,0,"0")
mse.setdPiFj(1,0,"0")
mse.buildModel()
mse.buildModelParams()
mse.buildWVarf()
mse.printTSOneStepW()
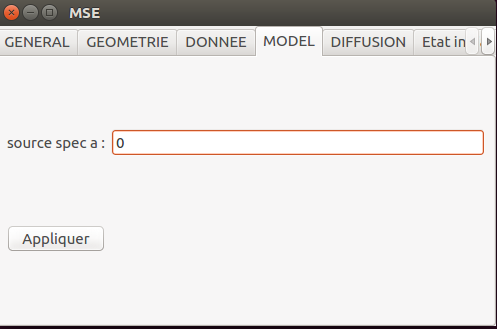
Définition de la diffusion hétérogène :
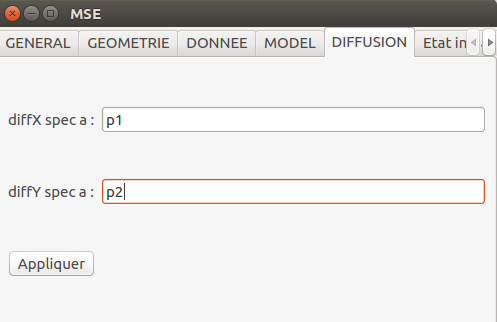
mse.setdpiDiffusionxExp(0,0,0,"1")
mse.setdpiDiffusionxExp(1,0,0,"0")
mse.setDiffusionyExp(0,0,"p2")
mse.setdpiDiffusionyExp(0,0,0,"0")
mse.setdpiDiffusionyExp(1,0,0,"1")
mse.buildDiffusion()
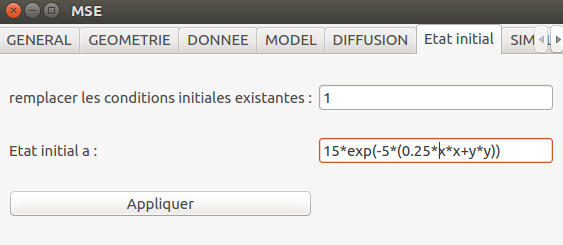
L'état initial est défini de la façon suivante :
mse.initInitialState()
mse.setIntParam(mse.MSE_KEY_FORCE_INITIAL_STATE,1)
mse.setInitialState(0,0,"10*exp(-5*(0.25*s*s+t*t))")
mse.setdPICiFj(0,0,"0")
mse.setdPICiFj(1,0,"0")
mse.printInitialState()
Définition des paramètres du simulateur
On choisit de simuler sur la période de temps [0,1], avec un pas de temps fixe égale à 0.05. La non-linéarité sera gérée par un algorithme de Newton-Raphson et une tolérance absolue de 0.02.
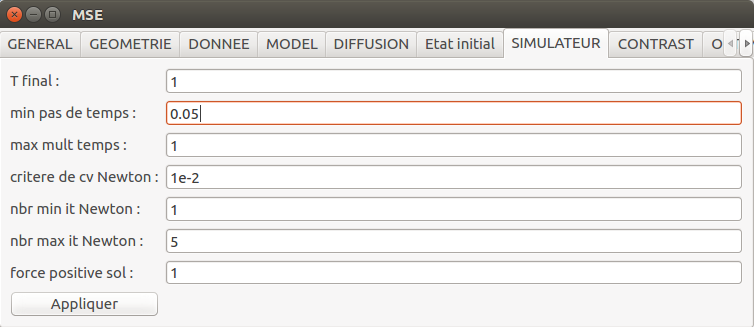
mse.setRealParam(mse.MSE_KEY_SIM_MINSTEP,0.05)
mse.setIntParam(mse.MSE_KEY_SIM_MAXMULTSTEP,1)
mse.setRealParam(mse.MSE_KEY_SIM_NEWTON_CRIT,0.01)
mse.setIntParam(mse.MSE_KEY_SIM_NEWTON_MIN_IT,1)
mse.setIntParam(mse.MSE_KEY_SIM_NEWTON_MAX_IT,5)
mse.setIntParam(mse.MSE_KEY_SIM_FORCE_POSITIV,1)
mse.buildTS()
Description des données
Pour construire des données simulées, une simulation avec (p1,p2)=(1,0.1) est effectuée pour obtenir en chaque point de l'espace la densité de population notée 'a'. Puis pour chaque lieu d'observation, Xloc, un tirage dans une loi de Bernoulli de paramètre 1-(1-p3 )S(aXloc) est effectué, avec un taux de détection p3=0.7 et la surface du piège S=0.2.
Il y a 15 pièges et 7 dates d'observations. Pour cela, il faut créer les fichiers de description comme décrit dans le tutoriel 'condition initiale paramétrée'.
Les données étant construites comme une réalisation d'un processus aléatoire, la recherche des paramètres optimaux (p1,p2,p3) ne donnera pas exactement les valeurs précédemment énoncées.