Introduction
Ce tutoriel illustre la mise en oeuvre de l'analyse de sensibilité sur un modèle paramétré par 5 paramètres. Les paramètres p1 et p2 représentent la diffusion horizontale et verticale, le paramètre p3 est le taux de croissance, le paramètre p4 est la capacité du milieu, p5 représente le taux de mortalité dans la zone hostile.
La zone d'étude est un rectangle dont la moitié droite porte un taux de mortalité p5.
La suite de cette page décrit comment mener cette étude dans MSE, d'une part via l'interface, d'autre part via un script python.
Description de l'étude
Il s'agit donc d'une étude portant sur 1 espèce paramétrée par 5 paramètres :
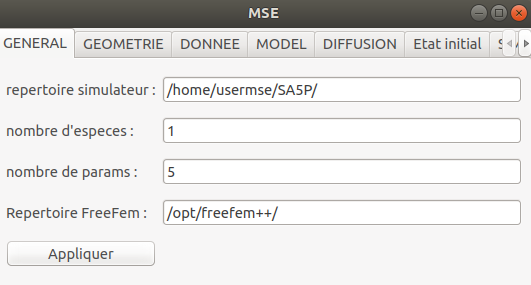
import mse
MY_OUTPUT_DIR=os.getenv("MSE_OUTPUT_DIR", "/home/mseuser/MSE/demoSA5P/")
mse.setStringParam(mse.MSE_KEY_OUTPUT_DIR,MY_OUTPUT_DIR)
mse.setIntParam(mse.MSE_KEY_MODEL_NBSPECIES,1)
mse.setIntParam(mse.MSE_KEY_MODEL_NBPARAMS,5)
Description de la zone d'étude
La zone d'étude est le rectangle [-2,2]x[-1,1]. La triangulation sera créée à partir de 30 points par unité de longueur des arêtes :
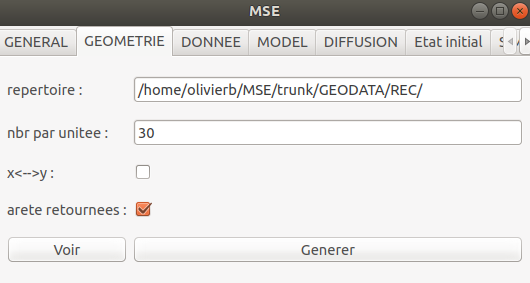
mse.setStringParam(mse.MSE_KEY_GEOM_DIR,MY_GEOM_DIR)
mse.setRealParam(mse.MSE_KEY_GEOM_NPERLENGTH,30.0)
mse.setIntParam(mse.MSE_KEY_GEOM_SYM,0)
mse.setIntParam(mse.MSE_KEY_GEOM_REVEDGE,1)
mse.buildGeom()
mse.buildDirectories()
os.system("cd "+MY_OUTPUT_DIR+";/opt/freefem++/src/nw/FreeFem++-nw "+MY_OUTPUT_DIR+"/buildXY.edp")
Description du modèle de réaction-diffusion
Le modèle étudié est de la forme :
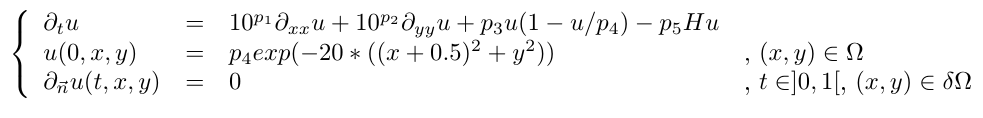
Où H est définie dans le fichier loadHerogenData.edp. H est nulle sur la moitié gauche du domaine et vaut 1 sur la partie droite (loadHerogenData.edp).
Le coefficient de diffusion :
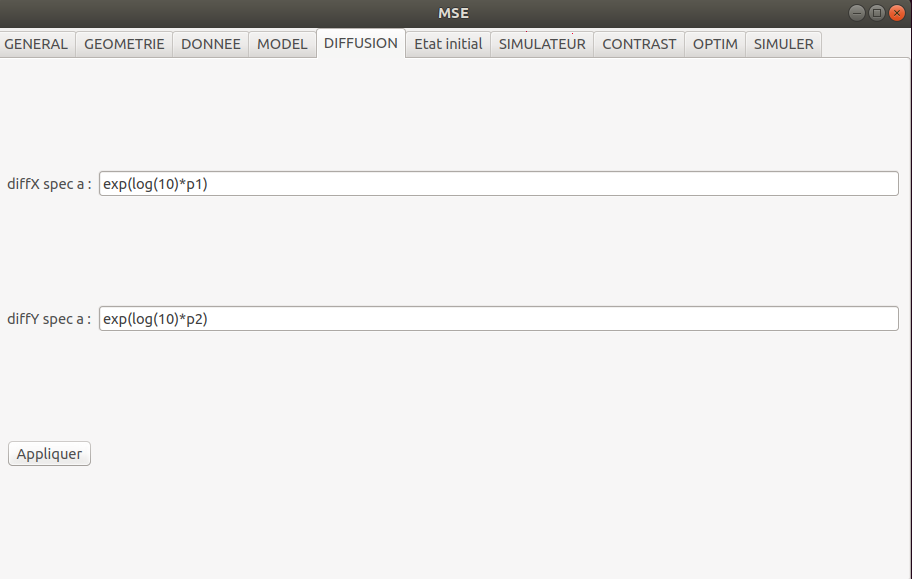
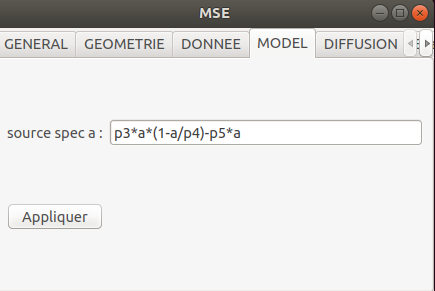
Le terme de réaction :
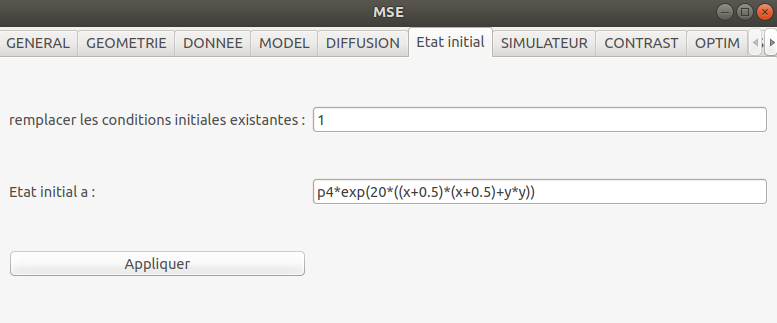
La condition initiale :
mse.initGradEdp()
mse.setfxExp(0,"p3*a*(1-a/p4)-p5*H*a")
mse.setdyfxExp(0,0,"-a*p3/p4 + p3*(-a/p4 + 1) - p5*H")
mse.buildModel()
mse.setDefaultParamValue(0,-1)
mse.setDefaultParamValue(1,-1)
mse.setDefaultParamValue(2,0.5)
mse.setDefaultParamValue(3,1)
mse.setDefaultParamValue(4,0.5)
mse.buildModelParams()
mse.buildWVarf()
mse.printTSOneStepW()
mse.setDiffusionxExp(0,0,"exp(log(10.0)*p1)")
mse.setDiffusionyExp(0,0,"exp(log(10.0)*p2)")
mse.buildDiffusion()
mse.setIntParam(mse.MSE_KEY_FORCE_INITIAL_STATE,1)
mse.setInitialState(0,0,"p4*exp(-20*((x+0.5)*(x+0.5)+y*y))")
mse.printInitialState()
Définition des paramètres du simulateur
On choisit de simuler sur la période de temps [0,1], avec un pas de temps fixe égale à 0.05. La non-linéarité sera gérée par un algorithme de Newton-Raphson et une tolérance absolue de 0.02.
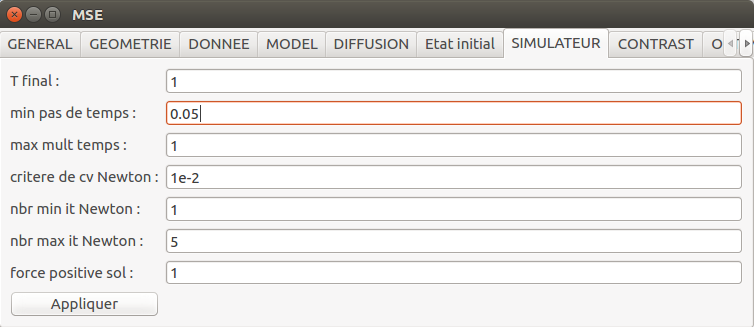
mse.setRealParam(mse.MSE_KEY_SIM_MINSTEP,0.05)
mse.setIntParam(mse.MSE_KEY_SIM_MAXMULTSTEP,1)
mse.setRealParam(mse.MSE_KEY_SIM_NEWTON_CRIT,0.01)
mse.setIntParam(mse.MSE_KEY_SIM_NEWTON_MIN_IT,1)
mse.setIntParam(mse.MSE_KEY_SIM_NEWTON_MAX_IT,5)
mse.setIntParam(mse.MSE_KEY_SIM_FORCE_POSITIV,1)
mse.buildTS()
Définition de la fonction à analyser
Le fichier 'functMesure.edp' implémente le calcul d'intégrale quadratique de la densité de population. Il s'agit de la fonction :
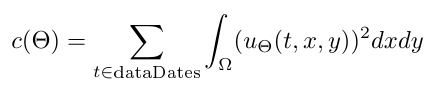
Mise en oeuvre de l'analyse de sensibilité
- définition des bornes des intervalles d'incertitude pour chaque paramètre
- choix de la méthode d'analyse de sensibilité et valeurs des arguments du plan d'expérience associé
1) méthode de Morris
mse.setIntParam(mse.MSE_KEY_SA_METHOD,mse.MSE_CST_MSE_AS_MORRIS);
mse.setIntParam(mse.MSE_KEY_SA_PARAM_NT,100);
mse.setIntParam(mse.MSE_KEY_SA_PARAM_ND,6);
mse.SABuildDesign()
mse.SAExecuteDesign()
mse.SAPerform()
2) méthode de Sobol
mse.SAInit()
mse.setSALowerBound(0,-3)
mse.setSALowerBound(1,-3)
mse.setSALowerBound(2,0.5)
mse.setSALowerBound(3,0.2)
mse.setSALowerBound(4,0.1)
mse.setSAUpperBound(0,-0.5);
mse.setSAUpperBound(1,-0.5);
mse.setSAUpperBound(2,10);
mse.setSAUpperBound(3,1);
mse.setSAUpperBound(4,10);
mse.setIntParam(mse.MSE_KEY_SA_METHOD,mse.MSE_CST_MSE_AS_SOBOL);
mse.setIntParam(mse.MSE_KEY_SA_PARAM_NP,400);
mse.buildVtkForVisu()
os.system("cp *.edp "+MY_OUTPUT_DIR)
mse.SABuildDesign()
mse.SAExecuteDesign()
mse.SAPerform()
Résultats
1- sorties numériques
Les résultats statistiques d'une méthode comprennent les indices de sensibilité et leurs intervalles de confiance (p=0.95).
1-1 méthode de Morris:
Les informations sont stockées dans le fichier Mindices.txt
p1 p2 p3 p4 p5
mu.star 0.4868300 0.2833504 1.255340 1.268133 0.13234860
Binf 0.3056470 0.2089863 1.007624 0.978145 0.06867762
Bsup 0.6680130 0.3577146 1.503055 1.558121 0.19601957
sigma 0.9234161 0.3800349 1.248431 1.461474 0.32088716
Binf 0.8107656 0.3336732 1.096131 1.283184 0.28174113
Bsup 1.0727096 0.4414771 1.450271 1.697758 0.37276668
1-2 méthode de Sobol:
Les informations sont stockées dans le fichier Sindices.txt
p1 p2 p3 p4 p5
IP 0.00000000 0.00000000 0.5021692 0.2491807 0.000000000
Binf 0.00000000 0.00000000 0.3844057 0.1627098 0.000000000
Bsup 0.08812058 0.07466497 0.6016804 0.3464366 0.090580792
IT 0.11723575 0.05265597 0.6839243 0.4682532 0.022323756
Binf 0.08435207 0.03533724 0.5564090 0.3567196 0.007414001
Bsup 0.15632431 0.06686737 0.7808957 0.5894151 0.034411654
2- sorties graphiques
2-1 méthode de Morris
- Indices
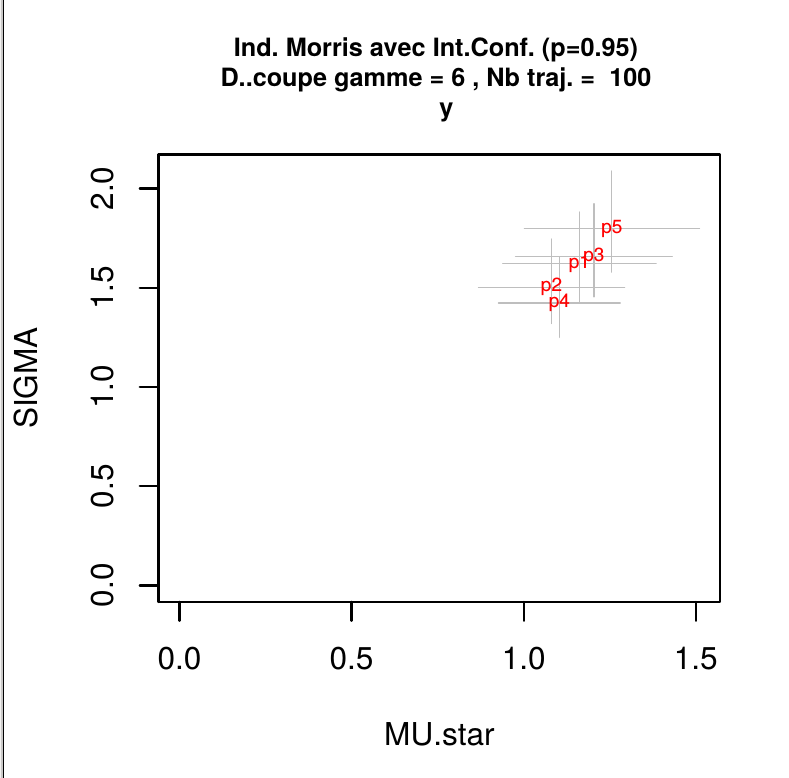
- Histogramme de la sortie et relation avec chacun des paramètres.
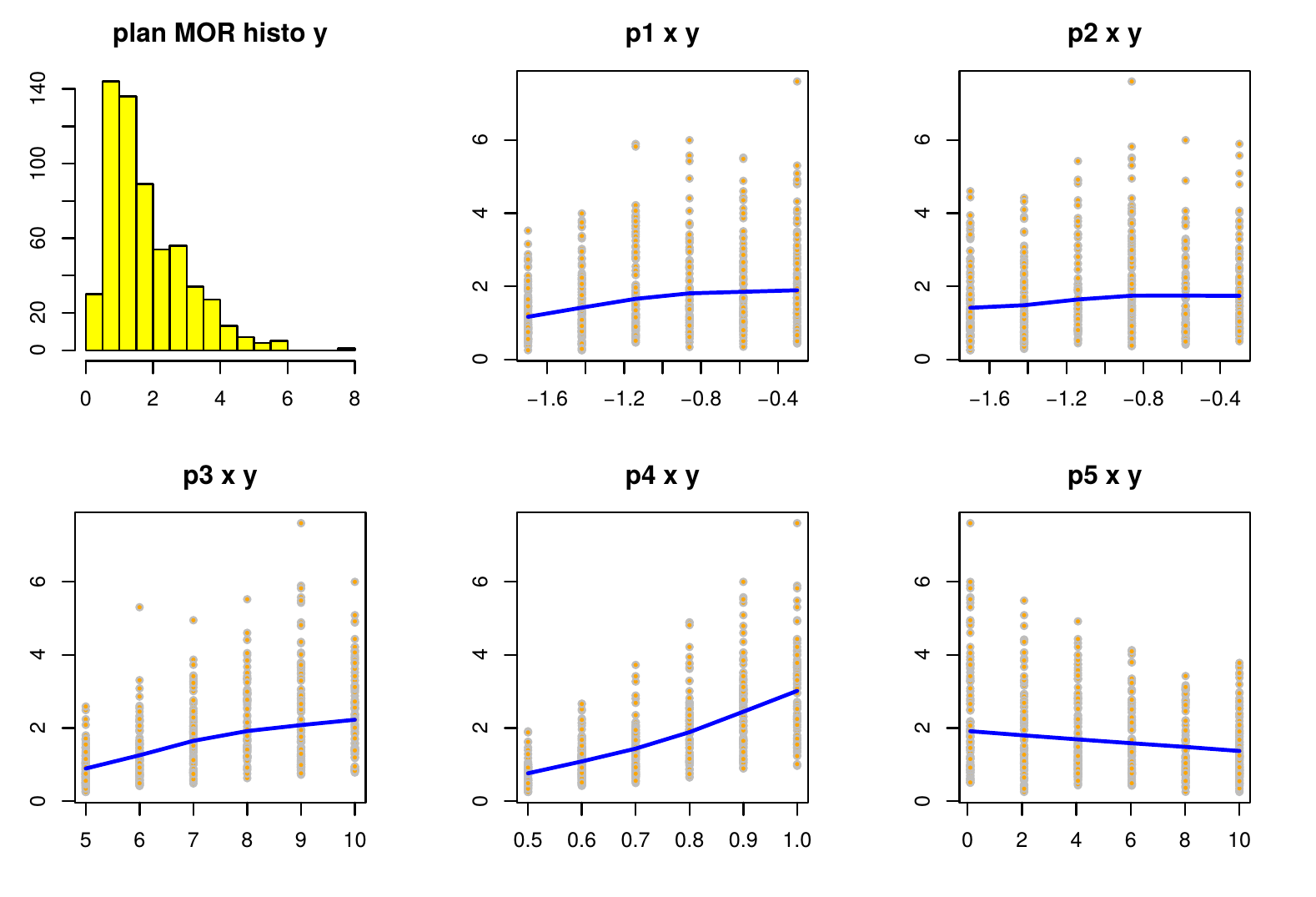
-Représentation des interactions d'ordre 2 (graphInterMor.pdf)
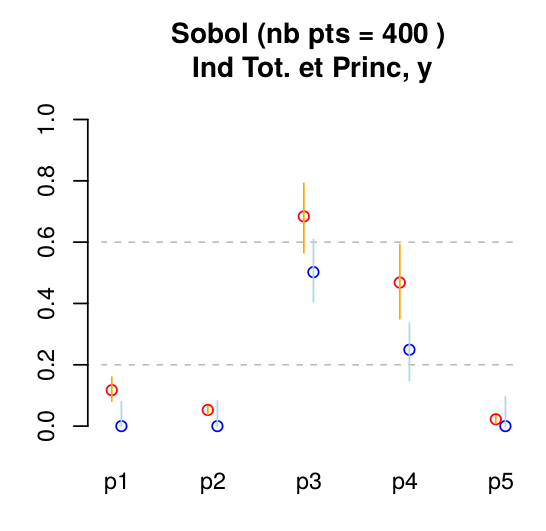
2-2 méthode de Sobol
Indices de sensibilité principaux (en bleu) et totaux (en rouge). L'indice principal caractérise
l'effet d'un paramètre sur la sortie dans la gamme d'incertitude. L'indice total
quantifie les effets principaux et d'interaction de différents ordres.
- Histogramme de la sortie et relation avec chacun des paramètres.
(grafParVar.pdf) :
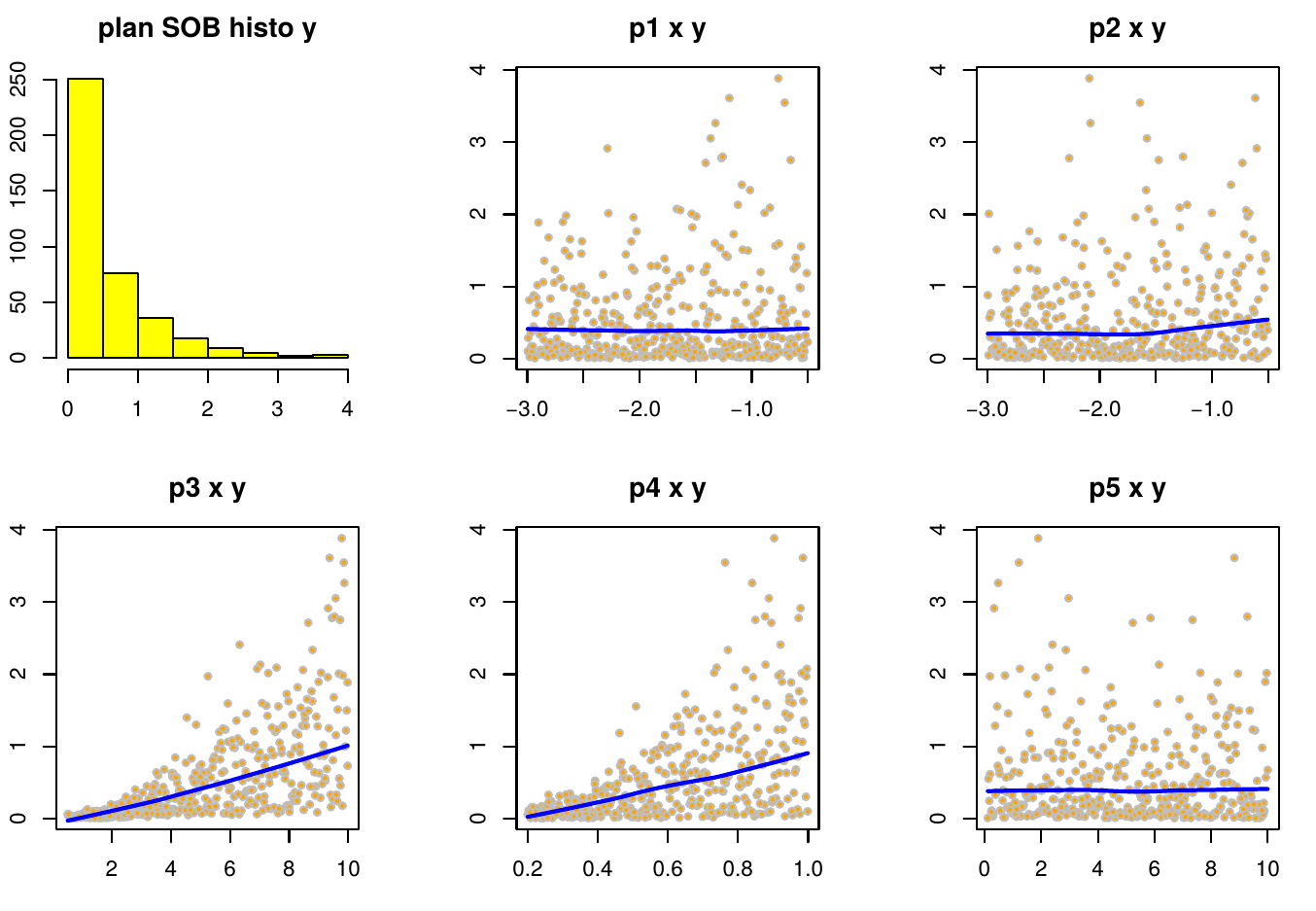
Les relations entre y et les paramètres p3 et p4 sont cohérentes avec les indices principaux observés.
- Représentation de l'interaction d'ordre 2 (grafInter.pdf) :
Soit à caractériser l'effet de l'interaction entre la sortie y et deux paramètres pi et pj.
On parlera d'interaction d'ordre 2. L'interaction d'ordre 2 n'est qu'une partie de l'interaction quantifiée
par l'indice total, mais elle est souvent prédominante et plus facile à interpréter.
Considérons l'espérance conditionnelle E( Y |pi , pj) de y sachant pi et pj. Elle est estimée par la régression
entre les résultats de simulation et les deux paramètres. Dire que qu'il n'y a pas d'interaction d'ordre 2 au sens statistique entre pi et pj revient à exprimer que les espérances E( Y |pi , pj=z) quand on fait varier z diffèrent seulement d'une constante. Cette idée est reprise dans les graphiques en la simplifiant. Sous l'hypothèse que les courbes E( Y |pi , pj=z) et E( Y |pi , pj=z') quand z et z' sont proches, la gamme d'incertitude de pj est décomposée en 4 intervalles disjoints (1 par couleur). On détermine ensuite dans chaque classe la régression entre y et pi. Quand il n'y a pas d'interaction les courbes sont sensiblement parallèles.
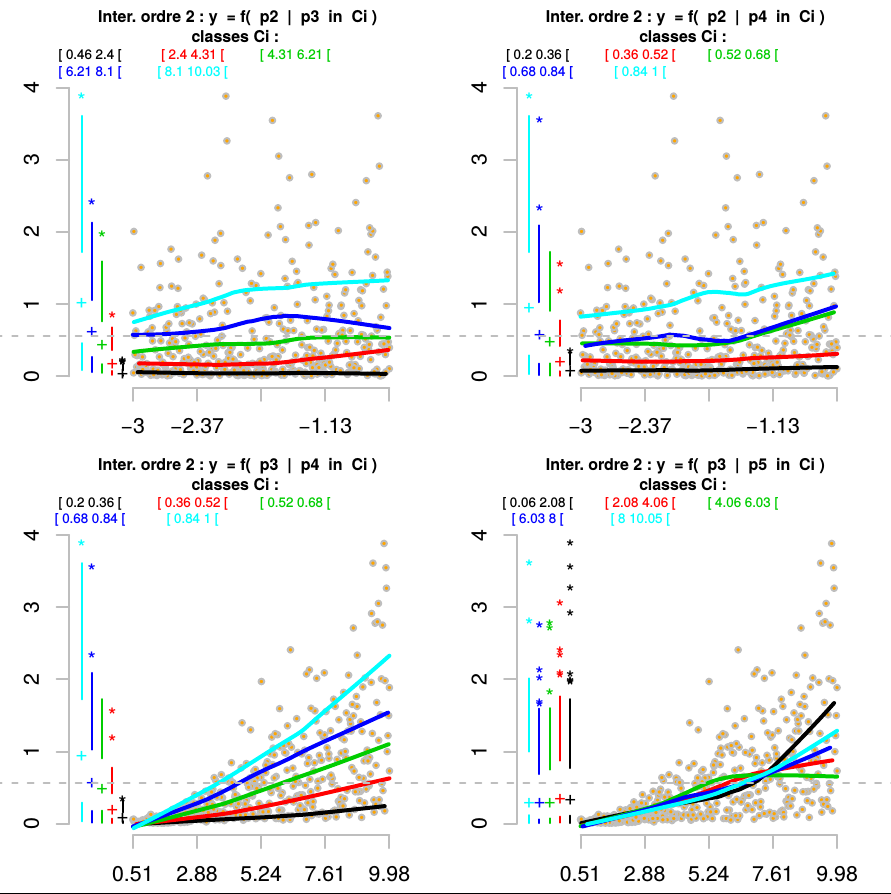
Les graphiques mettent en évidence une interaction d'ordre 2 des paramètres p3 et p4. Ceci est cohérent
avec l'importance de l'interaction mise en évidence par les indices totaux.
On peut noter sur le dernier graphique un effet d'interaction entre p3 et p5 quand p3> 7.61 environ. Ce phénomène n'est pas détecté par l'indice total de ces paramètres qui estime un effet moyen sur toute la gamme.
