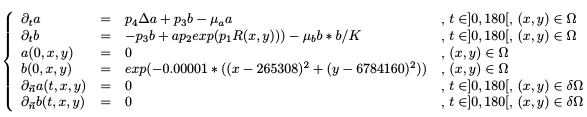Introduction
Il s'agit d'étudier les déplacements des larves et des imagos sur un bassin versant. Cette étude s'appuie sur des données d'abondance des larves. Le but de ce tutoriel est de modéliser ces déplacements par un modèle de réaction-diffusion hétérogène paramétré, puis d'ajuster le modèle. Dans un premier temps, l'étude portera sur des données simulées puis sera déclinée sur les données d'abondance.
La suite de cette page décrit comment mener cette étude dans MSE, d'une part via l'interface, d'autre part via un script python
Description de l'étude
Il s'agit d'une étude portant sur 2 espèces avec 1 paramètre :
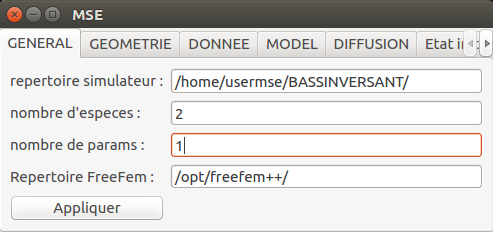
import mse
MY_OUTPUT_DIR=os.getenv("MSE_OUTPUT_DIR", "/home/usermse/BASSINVERSANT/")
mse.setStringParam(mse.MSE_KEY_OUTPUT_DIR,MY_OUTPUT_DIR)
mse.setIntParam(mse.MSE_KEY_MODEL_NBSPECIES,2)
mse.setIntParam(mse.MSE_KEY_MODEL_NBPARAMS,1)
Description de la zone d'étude
La géométrie du bassin versant est un polygone importé dans la bibliothèque géométrique de MSE par l'outils ImportPolygone.
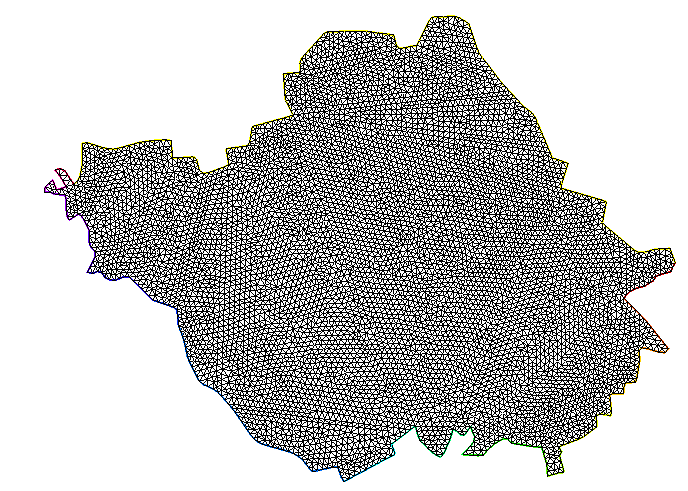
La zone d'étude le bassin versant :
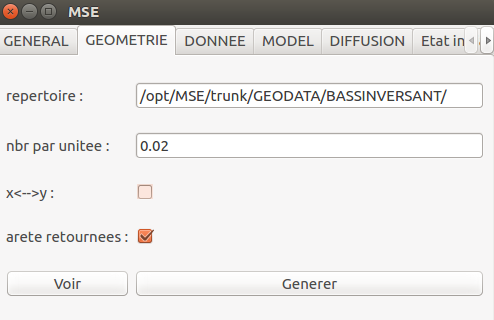
La discrétisation obtenue avec un point tout les 50 mètres est un maillage de 6950 points:
mse.setRealParam(mse.MSE_KEY_GEOM_NPERLENGTH,0.02)
mse.setIntParam(mse.MSE_KEY_GEOM_SYM,0)
mse.setIntParam(mse.MSE_KEY_GEOM_REVEDGE,1)
mse.buildGeom()
mse.initGradEdp()
mse.initModel()
mse.buildDirectories()
os.system("cd "+OUTPUT_DIR+";/opt/freefem++/src/nw/FreeFem++-nw "+OUTPUT_DIR+"/buildXY.edp")
Description du modèle de réaction diffusion
Le modèle étudié est le suivant :

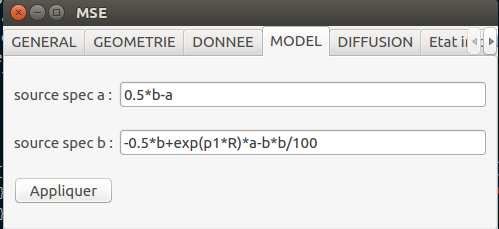
mse.setfxExp(0,"0.5*b-a")
mse.setdyfxExp(0,0,"-1")
mse.setdyfxExp(1,0,"0.500000000000000")
mse.setdPiFj(0,0,"0")
if (modelExp==1):
mse.setfxExp(1,"-0.5*b+exp(p1*R)*a-b*b/100")
mse.setdyfxExp(0,1,"exp(R*p1)")
mse.setdyfxExp(1,1,"-b/50 - 0.5")
mse.setdPiFj(0,1,"R*a*exp(R*p1)")
else:
mse.setfxExp(1,"-0.5*b+p1*R*a-b*b/100")
mse.setdyfxExp(0,1,"R*p1")
mse.setdyfxExp(1,1,"-b/50 - 0.5")
mse.setdPiFj(0,1,"R*a")
mse.buildModel()
mse.buildModelParams()
mse.buildWVarf()
mse.printTSOneStepW()
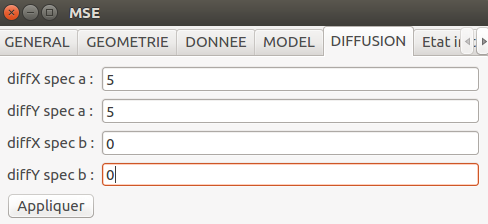
mse.setDiffusionxExp(0,0,"5")
mse.setdpiDiffusionxExp(0,0,0,"0")
mse.setDiffusionyExp(0,0,"5")
mse.setdpiDiffusionyExp(0,0,0,"0")
mse.setDiffusionxExp(1,0,"0")
mse.setdpiDiffusionxExp(0,1,0,"0")
mse.setDiffusionyExp(1,0,"0")
mse.setdpiDiffusionyExp(0,1,0,"0")
mse.buildDiffusion()
mse.setIntParam(mse.MSE_KEY_FORCE_INITIAL_STATE,1)
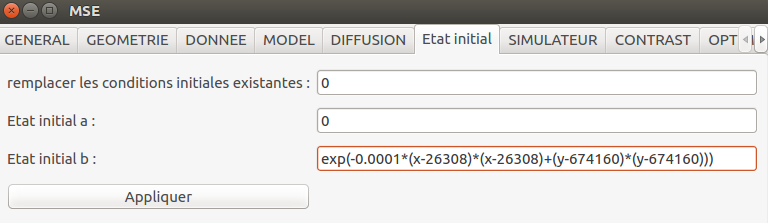
mse.setInitialState(0,0,"0")
mse.setdPICiFj(0,0,"0")
mse.setInitialState(0,1,"exp(-0.0001*(x-26308)*(x-26308)+(y-674160)*(y-674160)))")
mse.setdPICiFj(0,1,"0")
mse.printInitialState()
Comme décrit dans 'import d'une covariable spacialisée', la covariable R est importée à partir d'un raster de la manière suivante:
mse.setStringParam(mse.MSE_KEY_DATA_ADDCOV,"R")
os.system("cd /home/usermse/BASSINVERSANT/;/opt/freefem++/src/nw/FreeFem++ /home/usermse/BASSINVERSANT//showHeterogenCov.edp")
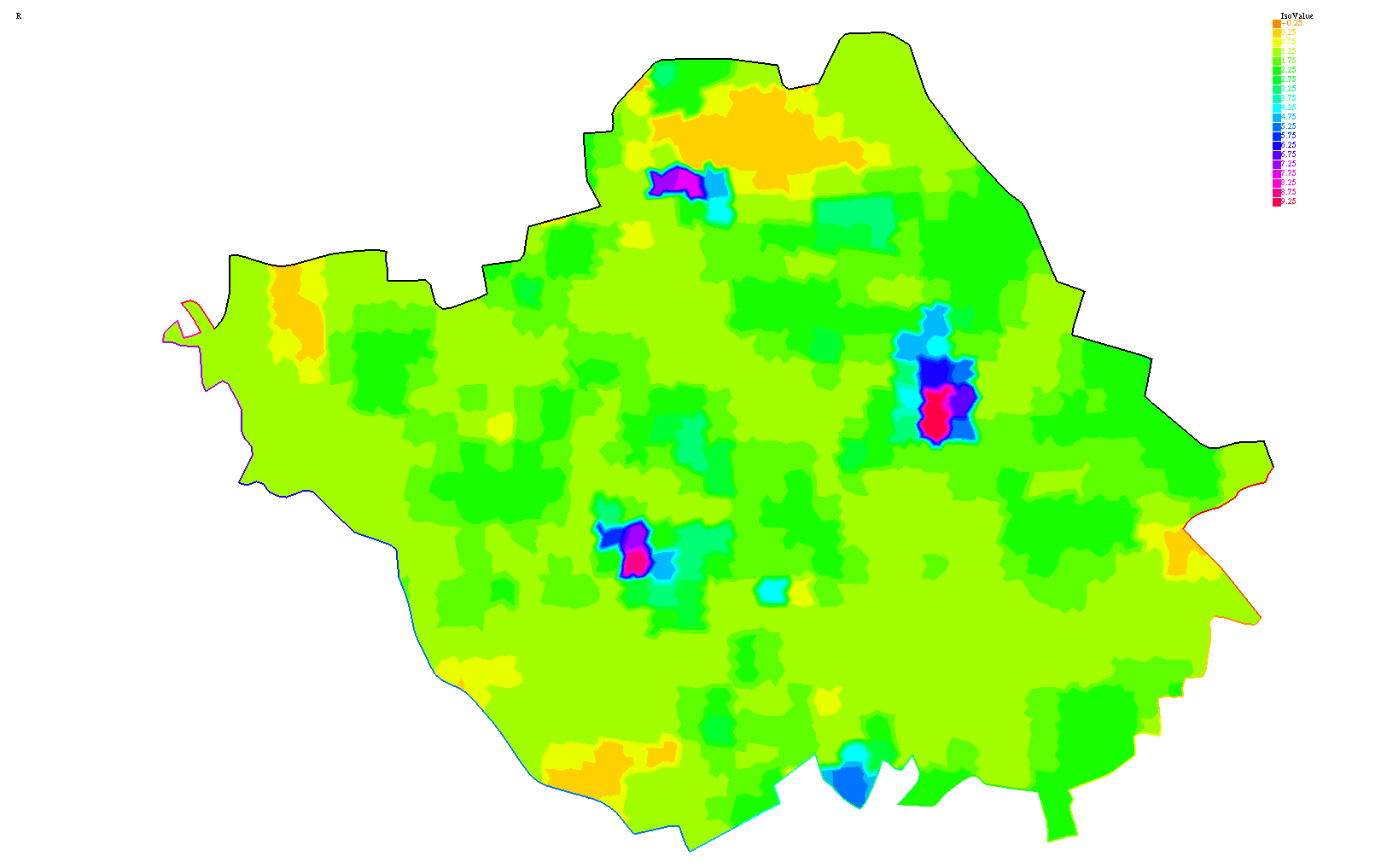
Définition des paramètres du simulateur
La période de simulation est de 180 jours. Le pas de temps varie de 0.1 j à 6.4 j et est ajusté selon la tolérance prescrite :
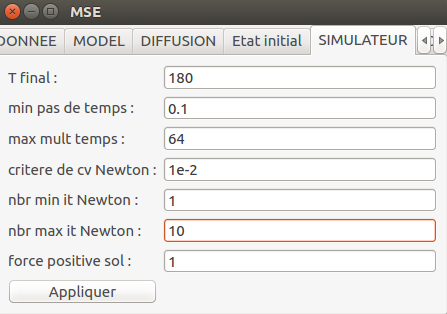
mse.setRealParam(mse.MSE_KEY_SIM_MINSTEP,0.1)
mse.setIntParam(mse.MSE_KEY_SIM_MAXMULTSTEP,64)
mse.setRealParam(mse.MSE_KEY_SIM_NEWTON_CRIT,0.01)
mse.setRealParam(mse.MSE_KEY_SIM_ADAPTIV_REL_ERROR,0.02)
mse.setIntParam(mse.MSE_KEY_SIM_NEWTON_MIN_IT,1)
mse.setIntParam(mse.MSE_KEY_SIM_NEWTON_MAX_IT,10)
mse.setIntParam(mse.MSE_KEY_SIM_FORCE_POSITIV,1)
mse.buildTS()
Définition de la fonction objectif à minimiser
Cas de données simulées
La trajectoire de référence a été obtenue avec le paramètre p1=0.2. Il s'agit alors de minimiser l'intégrale de la différence quadratique entre la simulation et la référence pour les pas de temps spécifiés.
La fonction de coût associé au paramètre (p1) est:
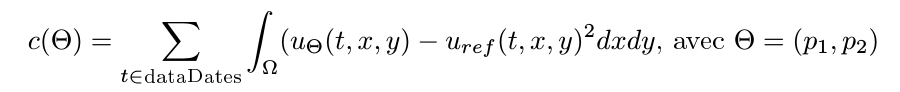
Avec uref la simulation de référence.
Cela se spécifie de la façon suivante dans l'interface :
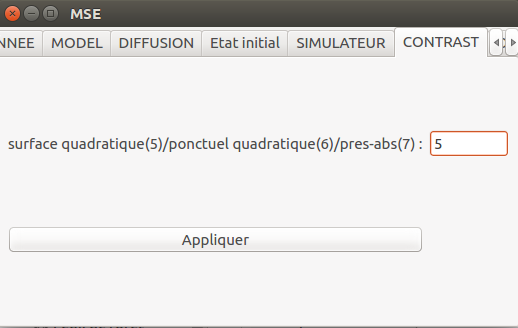
mse.buildContrast()
Cas des données d'abondance
à venir
Description du problème d'optimisation
Il s'agit d'un problème d'optimisation sous contraintes. Pour le résoudre, un algorithme de Quasi-Newton BFGS est couplé au simulateur. Il s'agit d'un algorithme itératif pour lequel le point de départ est précisé ainsi que les conditions de convergence :
mse.setBfgsLowerBound(0,-1)
mse.setBfgsUpperBound(0,0.3)
mse.setBfgsInitialState(0,0.15)
mse.setBfgsTol(1e-3)
mse.buildBfgs()
Résultat de l'optimisation
Cas des données simulées
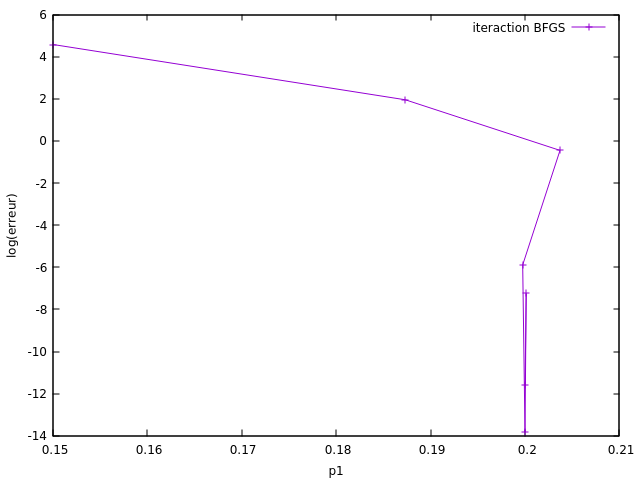
Dans ce cas, 4 itérations suffisent pour converger vers un optimum local (p1=0.20001 au lieu de 0.2) qui correspond aux données simulées.
L'animation suivante permet de visualiser la simulation pour le paramètre optimal.

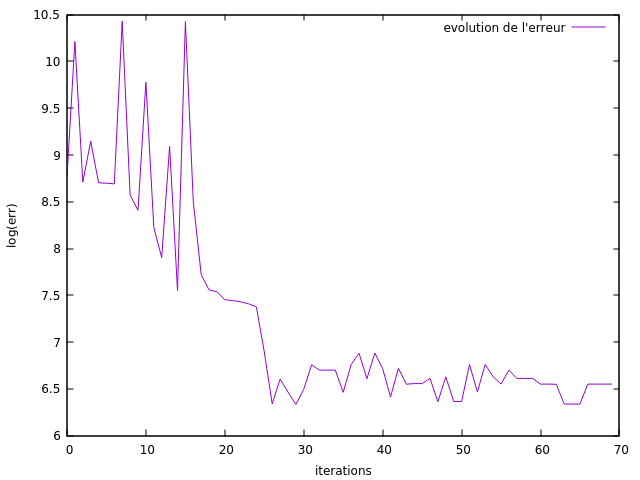
Dans le cas du modèle à 2 paramètres présenté ci-dessous, l'optimisation converge en 19 itérations vers l'optimum. Les figures suivantes montrent le comportement de l'algorithme d'optimisation.
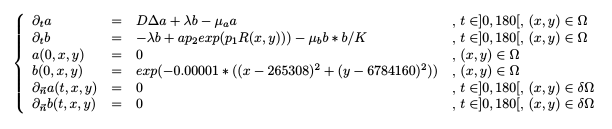
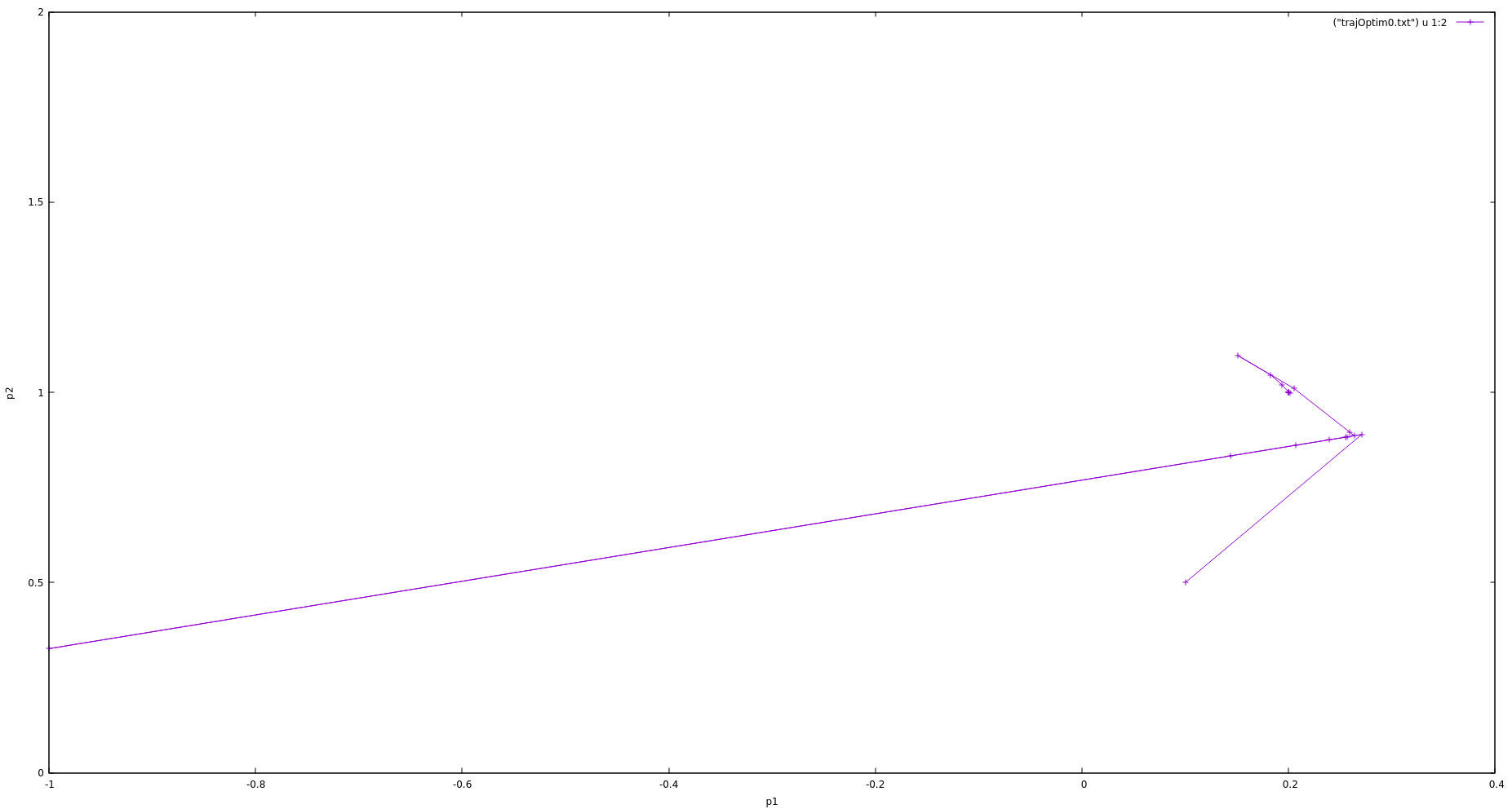
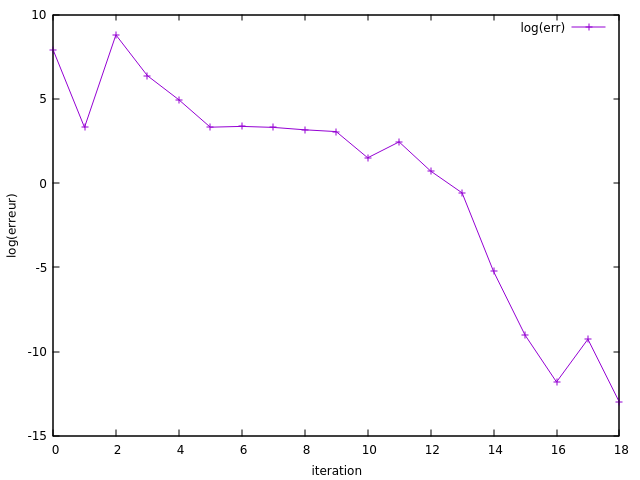
Dans le cas du modèle à 4 paramètres présenté ci-dessous, l'optimisation converge. Les figures suivantes montrent le comportement de l'algorithme d'optimisation. Les paramètres (p1,p2,p3) convergent vers les valeurs attendues, alors que l'algorithme ne parvient pas ajuster la valeur du coefficient de diffusion p4. Ce comportement semble montrer que le modèle se comporte surtout comme un modèle de réaction et peu comme un modèle de diffusion.